
Солнечно-земная
Физика
 |
Солнечно-земная
|  Статьи |
Область замкнутых силовых линий в магнитосфере содержит энергичные электроны, протоны и более тяжелые ионы в энергетическом интервале от нескольких кэВ до сотен МэВ (для протонов) и называется радиационным поясом (поясами) Земли. Частицы радиационных поясов захвачены геомагнитным полем и оставались бы в нем неопределенно долго, если бы не действие механизмов диффузии, ускорения и потерь.
Многие динамические процессы, поддерживающие существование радиационных поясов, в основном известны. Мелкомасштабные флуктуации электрического и магнитного полей вызывают радиальную диффузию этих частиц. Поскольку чисто диффузионный поток направлен при этом радиально к Земле, т.е. в область более высокой напряженности магнитного поля, частицы в дальнейшем ускоряются под действием бетатронного механизма. Наряду с этим резонансное взаимодействие низкоэнергичных частиц (осциллирующих и прецессирующих в геомагнитном поле) с гидромагнитными и ОНЧ-волнами вызывает диффузию вдоль магнитных силовых линий. Новый поток направлен от вершины силовой линии на экваторе к ее корням в атмосфере. Таком механизм диффузии по питч-углам. Когда захваченная частица высыпается в атмосферу, она быстро теряет свою энергию на ионизацию окружающей среды и таким образом выходит из состава радиационных поясов. Поэтому очевидно, что диффузия по питч-углам управляет механизмом потерь этих частиц.
Менее очевиден следующий факт: частицы и волны настолько эффективно взаимодействуют во внешней магнитосфере, что их потоки взаимозависимы. Например, если поток частиц возрастает выше определенного предела, волны усиливаются так, что соответствующее увеличение диффузии по питч-углам приводит к высыпанию из радиационного пояса избыточных частиц. Экспериментальные результаты говорят, что значения потоков частиц во внешней магнитосфере никогда не превышают пределов, определяемых взаимодействием волн с частицами. [1]
Взятые вместе, вышеперечисленные факты говорят о важности знания питч-углового распределения для уточнения механизмов потерь частиц, как во внешней магнитосфере, так и во внутренней, где одним из важнейших внешних факторов является атмосфера Земли.
При рассмотрении движения частицы или ее ведущего центра вдоль выделенной силовой линии можно использовать сохранение магнитного момента
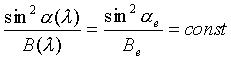 (1)
(1)
Где ![]() и
и ![]() - питч-угол и модуль магнитного
поля на широте
- питч-угол и модуль магнитного
поля на широте ![]() ;
; ![]() и
и ![]() - питч-угол и модуль магнитного поля в
начальной точке, вообще говоря, произвольной, за которую можно выбрать экватор.
В данном соотношении предполагается постоянство скорости
- питч-угол и модуль магнитного поля в
начальной точке, вообще говоря, произвольной, за которую можно выбрать экватор.
В данном соотношении предполагается постоянство скорости ![]() вдоль силовой линии. Если инжектировать
частицу с питч-углом
вдоль силовой линии. Если инжектировать
частицу с питч-углом ![]() в
точку, где напряженность поля
в
точку, где напряженность поля ![]() , она будет навиваться на силовую линию, двигаясь вдоль последней со
скоростью, определяемой выражениями
, она будет навиваться на силовую линию, двигаясь вдоль последней со
скоростью, определяемой выражениями
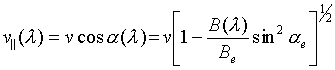 (2)
(2)
Если частица перемещается в область большей напряженности
магнитного поля, то ![]() будет
уменьшаться. Когда она достигнет точки, где поле имеет величину
будет
уменьшаться. Когда она достигнет точки, где поле имеет величину
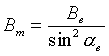 (3)
(3)
параллельная составляющая скорости обратится в нуль. В этом
случае движение частицы происходит только в направлении, перпендикулярном полю,
и ее питч-угол равен ![]() . Кроме
того, существуют следующие соотношения
. Кроме
того, существуют следующие соотношения
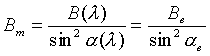 (4)
(4)
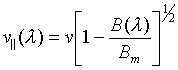 (5)
(5)
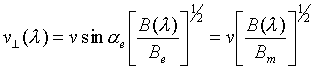 (6)
(6)
Заметим, что положение точки отражения, определяемое модулем
магнитного поля в этой точке ![]() не зависит от параметров рассматриваемой частицы (если не считать ее
начальное положение и начальный питч-угол). Точки отражения определяются
исключительно геометрией магнитного поля, если силовые линии являются
эквипотенциалями (параллельная составляющая силы отсутствует).
не зависит от параметров рассматриваемой частицы (если не считать ее
начальное положение и начальный питч-угол). Точки отражения определяются
исключительно геометрией магнитного поля, если силовые линии являются
эквипотенциалями (параллельная составляющая силы отсутствует).
Выше не конкретизировалась конфигурация поля. Теперь рассмотрим простейший случай - дипольное поле, определяемое соотношением
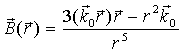 (7)
(7)
где ![]() -
радиус-вектор некоторой точки пространства, где измеряется поле,
-
радиус-вектор некоторой точки пространства, где измеряется поле, ![]() -вектор магнитного момента точечного
магнитного диполя. Тогда модуль напряженности поля
-вектор магнитного момента точечного
магнитного диполя. Тогда модуль напряженности поля ![]() вдоль выделенной силовой линии как функция
широты равен
вдоль выделенной силовой линии как функция
широты равен
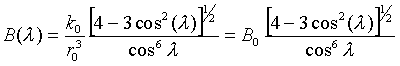 (8)
(8)
где
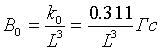 (9)
(9)
- напряженность поля на экваторе.
Если инжектировать в дипольное поле частицу с экваториальным
питч-углом ![]() , она будет
колебаться вдоль силовой линии между точками отражения, определяемыми (4).
Комбинируя (4) и (8) можно определить широту
, она будет
колебаться вдоль силовой линии между точками отражения, определяемыми (4).
Комбинируя (4) и (8) можно определить широту ![]() точек отражения, решив (численно)
уравнение
точек отражения, решив (численно)
уравнение
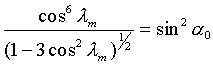 (10)
(10)
Заметим, что для данного ![]() широта
широта ![]() не зависит от конкретной силовой линии
(
не зависит от конкретной силовой линии
(![]() или
или ![]() ). Другими словами, все частицы с данным
экваториальным питч-углом
). Другими словами, все частицы с данным
экваториальным питч-углом ![]() отражаются в дипольном поле при одной и той же широте
отражаются в дипольном поле при одной и той же широте ![]() , не связанной с местоположением ведущих
силовых линий, на которых они находятся.
, не связанной с местоположением ведущих
силовых линий, на которых они находятся.
Для земного дипольного поля существует верхний предел для
величины ![]() : точка отражения
частицы всегда должна лежать выше земной поверхности (фактически выше плотных
слоев атмосферы):
: точка отражения
частицы всегда должна лежать выше земной поверхности (фактически выше плотных
слоев атмосферы):
![]() (11)
(11)
где ![]() определяется формулой
определяется формулой
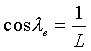 (12).
(12).
![]() - это
широта на которой силовая линия с параметром
- это
широта на которой силовая линия с параметром ![]() пересекает поверхность Земли.
пересекает поверхность Земли.
Следовательно, экваториальный питч-угол должен удовлетворять неравенству
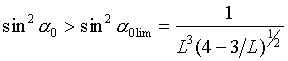 (13)
(13)
Предельный питч-угол ![]() равен половине угла раствора так называемого экваториального конуса
потерь: частицы, питч-угол которых лежит внутри конуса потерь, должны погибнуть
в плотной атмосфере прежде, чем смогут достичь своей точки отражения. Для
силовых линий близких к поверхности Земли
равен половине угла раствора так называемого экваториального конуса
потерь: частицы, питч-угол которых лежит внутри конуса потерь, должны погибнуть
в плотной атмосфере прежде, чем смогут достичь своей точки отражения. Для
силовых линий близких к поверхности Земли ![]() , раствор конуса потерь близок к
, раствор конуса потерь близок к ![]() .
.
Навиваясь на дипольную силовую линию, частица имеет локальный
питч-угол ![]() , связанный
соотношением (4) с экваториальным питч-углом
, связанный
соотношением (4) с экваториальным питч-углом ![]() :
:
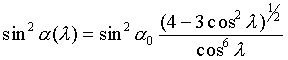 (14)
(14)
Этот питч-угол растет до ![]() при
при ![]() . При удалении частицы от экватора
расширяется и конус потерь:
. При удалении частицы от экватора
расширяется и конус потерь:
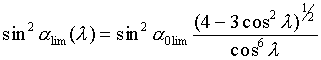 (15)
(15)
его угол раствора стремится к ![]() при
при ![]() .
.
Введем понятие направленного потока частиц. Определим
направленный поток ![]() частиц
данного сорта с заданной энергией как число частиц, приходящих с заданного
направления в единицу времени. Поток рассматривается в единичном интервале
телесного угла и в единичном интервале на поверхности единичной площадки,
ориентированной перпендикулярно направлению прихода частиц. В самом общем случае
частиц
данного сорта с заданной энергией как число частиц, приходящих с заданного
направления в единицу времени. Поток рассматривается в единичном интервале
телесного угла и в единичном интервале на поверхности единичной площадки,
ориентированной перпендикулярно направлению прихода частиц. В самом общем случае
![]() для данного сорта частиц
будет функцией энергии
для данного сорта частиц
будет функцией энергии ![]() ,
координат
,
координат ![]() , направления
прихода
, направления
прихода ![]() и времени
и времени ![]() :
:
![]() . (16)
. (16)
Величина ![]() содержит в себе полную информацию относительно распределения частиц в
пространстве (
содержит в себе полную информацию относительно распределения частиц в
пространстве (![]() ), по
направлениям скорости (
), по
направлениям скорости (![]() ) и
по энергии (
) и
по энергии (![]() ) в заданный
момент времени. Величина (16) это то, что измерял бы идеальный направленный
детектор. В отсутствие взаимодействия между частицами и их группами
) в заданный
момент времени. Величина (16) это то, что измерял бы идеальный направленный
детектор. В отсутствие взаимодействия между частицами и их группами ![]() не должно содержать никакой
явной зависимости от времени. Кроме того, при таких условиях поток частиц с
некоторого заданного направления
не должно содержать никакой
явной зависимости от времени. Кроме того, при таких условиях поток частиц с
некоторого заданного направления ![]() равен потоку с противоположного направления:
равен потоку с противоположного направления:
![]() . (17)
. (17)
С учетом конечных угловых размеров детекторов вводят и другую величину - всенаправленный поток, который определяют как
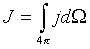 . (18)
. (18)
Последний представляет собой полное число частиц с заданной
энергией, которые приходят в единицу времени со всех направлений и пересекают
сферу с единичной площадью поверхности. Детектор, скорость счета которого
пропорциональна ![]() (18),
называют всенаправленным детектором.
(18),
называют всенаправленным детектором.
Рассмотрим свойства направленного и всенаправленного потока.
Выберем направление магнитного поля в качестве полярной оси сферической системы
координат. Направление прихода ![]() определяется двумя углами: питч-углом
определяется двумя углами: питч-углом ![]() и азимутальным углом
и азимутальным углом ![]() . Если частицы равномерно распределены по
фазе циклотронного движения, то в заданной точке
. Если частицы равномерно распределены по
фазе циклотронного движения, то в заданной точке ![]() поток не будет зависеть от
поток не будет зависеть от ![]() . Это значит, что поток
. Это значит, что поток ![]() будет функцией только питч-угла частицы.
Число частиц с питч-углами
будет функцией только питч-угла частицы.
Число частиц с питч-углами ![]() в интервале от
в интервале от ![]() до
до ![]() , проходящих через точку
, проходящих через точку ![]() за 1 с со всех азимутальных
направлений
за 1 с со всех азимутальных
направлений ![]() , в расчете на
единичную площадку, перпендикулярную к направлению прихода и на единичный
интервал определяется формулой:
, в расчете на
единичную площадку, перпендикулярную к направлению прихода и на единичный
интервал определяется формулой:
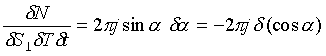 (19)
(19)
Изотропным потоком называется такой поток, в котором число приходящих частиц зависит только от угла раствора приемного детектора и не зависит от направления прихода.:
![]() (относительно
(относительно ![]() )
)
или
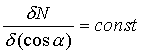 (20).
(20).
Последнее выражение показывает, что при изотропном
распределении одинаковое число частиц приходится на одинаковые интервалы
изменения косинуса питч-угла (а не самого питч-угла). Вот почему гистограммы
питч-углового распределения обычно строятся для переменной ![]() :
:
![]() (21).
(21).
Теперь обратимся к вопросу о том, как направленный поток данной
группы частиц изменяется вдоль данной силовой трубки, образованной силовыми
линиями от площадки 1 до площадки 2, а также вдоль всей дрейфовой оболочки,
образуемой этими частицами. Теорема Лиувилля для захваченных частиц говорит, что
плотность частиц в фазовом пространстве ![]() остается постоянной вдоль динамической
траектории частиц или:
остается постоянной вдоль динамической
траектории частиц или:
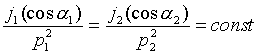 (22а)
(22а)
Для нерелятивистских частиц можно также написать:
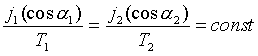 (22б)
(22б)
Если ![]() не
меняется во времени, и силовые линии представляют собой эквипотенциали, либо
если вообще отсутствуют внешние силы, то
не
меняется во времени, и силовые линии представляют собой эквипотенциали, либо
если вообще отсутствуют внешние силы, то
![]() (22в)
(22в)
Можно показать, что соотношения (22) остаются верны и в любой точке на дрейфовой оболочке.
Каждому питч-углу ![]() в заданной точке
в заданной точке ![]() на силовой линии соответствует некоторое значение питч-угла
на силовой линии соответствует некоторое значение питч-угла ![]() в экваториальной точке этой силовой линии.
Если поле потенциально, то связать и можно, используя (4):
в экваториальной точке этой силовой линии.
Если поле потенциально, то связать и можно, используя (4):
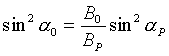 . (23)
. (23)
Знание питч-углового распределения ![]() у экватора позволяет найти питч-угловое
распределение и интегральный поток в любой другой точке силовой линии. Это
обусловлено тем, что любая частица, колеблющаяся вдоль силовой линии, непременно
должна проходить через экваториальную точку.
у экватора позволяет найти питч-угловое
распределение и интегральный поток в любой другой точке силовой линии. Это
обусловлено тем, что любая частица, колеблющаяся вдоль силовой линии, непременно
должна проходить через экваториальную точку.
С использованием приведенного выше равенства можно записать:
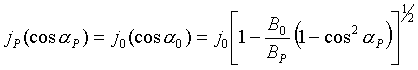 (24).
(24).
Таким образом, изотропное распределение в экваториальной плоскости приводит к изотропному же распределению всюду вдоль силовой линии.
Поток (24) обрезан при некотором нижнем предельном значении
угла ![]() , который представляет
собой половину угла раствора конуса потерь. Частицы с питч-углами
, который представляет
собой половину угла раствора конуса потерь. Частицы с питч-углами ![]() должны были бы отразиться под земной
поверхностью или ниже поглощающего слоя атмосферы, а поэтому не могут
существовать даже один полный период осцилляций между точками отражений.
должны были бы отразиться под земной
поверхностью или ниже поглощающего слоя атмосферы, а поэтому не могут
существовать даже один полный период осцилляций между точками отражений.
Пусть ![]() -
напряженность поля в точке пересечения с этим поглощающим атмосферным слоем,
который, как считается, расположен на высоте 100 км от земной поверхности, тогда
для половинного раствора конуса потерь
-
напряженность поля в точке пересечения с этим поглощающим атмосферным слоем,
который, как считается, расположен на высоте 100 км от земной поверхности, тогда
для половинного раствора конуса потерь ![]() в данной точке
в данной точке ![]() получим
получим
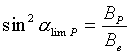 (25)
(25)
это означает, что
![]() при
при ![]() или
или 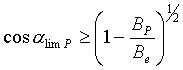
Всенаправленный поток (18) в точке ![]() на силовой линии, выраженный в виде
функции от локального
на силовой линии, выраженный в виде
функции от локального ![]() ,
запишется следующим образом:
,
запишется следующим образом:
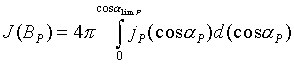
Это выражение можно преобразовать в интеграл от экваториального потока, если учесть (24) и проследить за соответствующими пределами интегрирования:
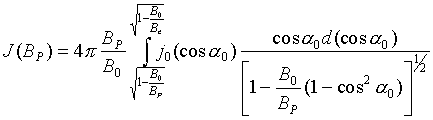 . (26)
. (26)
И, наконец, перпендикулярный поток ![]() в данной точке
в данной точке ![]() на силовой линии связан с
на силовой линии связан с ![]() формулой
формулой
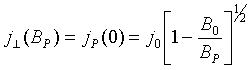 (27)
(27)
Формулы (24), (26) и (27) показывают, как по направленному потоку в экваториальной точке можно определить все, что относится к потокам частиц во всех других точках силовой линии.
Соотношение (26) можно преобразовать в интеграл вдоль силовой линии:
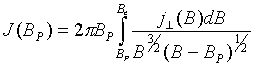 (28)
(28)
Можно получить и обратное соотношение:
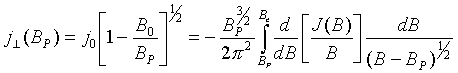 (29)
(29)
Если мы знаем всенаправленный поток вдоль всей силовой линии от
экватора до земной поверхности, то можем рассчитать и направленный поток ![]() (т.е. питч-угловое
распределение) у экватора и в любой промежуточной точке с помощью выражений (28)
и (29):
(т.е. питч-угловое
распределение) у экватора и в любой промежуточной точке с помощью выражений (28)
и (29):
Переход на другие страницы проекта "СиЗиФ"
 |
 |  |
 |
 |