
|
Солнечно-земная Физика
Справочник |
Адиабатические инварианты - физические величины, остающиеся практически неизменными при медленном (адиабатическом),
но не обязательно малом изменении внешних условий, в которых находится система, либо самих характеристик системы.
Отмеченное изменение должно происходить за времена, значительно превышающие характерные периоды движения системы.
В классической механике адиабатическими инвариантами являются переменные действия I=[интергал по замкнотому
контуру] pkdqk, где pk - обобщенный импульс, qk -
обобщенная координата, интегрирование производится по периоду (или квазипериоду).
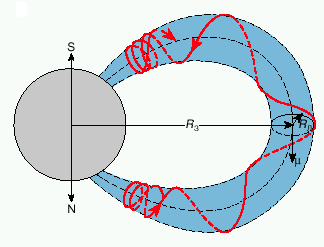
В магнитосфере Земли движение заряженных частиц с энергией меньше ∼1 ГэВ можно описать суперпозицией трех квазипериодических
движений - ларморовским вращением вокруг силовой линии, скачками между магнитными (зеркальными) пробками и дрейфовым вращением вокруг
Земли. Каждое из этих периодичаских движений может быть адиабатическим, если в данной области магнитосферы характерное
время изменения магнитного поля много больше периода вращения частицы данной энергии и пространственные неоднородности поля достаточро
малы на характерных размерах вращения.
Первым периодическим движением частицы является ларморовское (или циклотронное) вращение вокруг силовой линии и
а первым адиабатическим инвариантом - магнитный момент
частицы
Ларморовское вращение совершается с периодом τ, который определяется из равенства центробежной силы и
силы Лоренца.
![]()
На практике можно использовать формулу
![]()
где Е - кинетическая энергия частицы в МэВ, Е0 - энергия покоя
частицы в МэВ (для электрона Е0= 0.51 МэВ, для протона Е0= 938
МэВ) и В – магнитное поле в нТ.
Ларморовская частота 1/τ1 электронов вблизи Земли ~1 MГц,
протонов – ~1 кГц, при удалении от Земли частота уменьшается
как 1/Rз. Ларморовский радиус вращения частицы
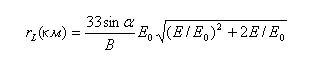
где В выражено в нТ, Е и Е0 в МэВ.
Ларморовский радиус электронов радиационных поясов в
геомагнитном поле не превосходит нескольких километров, а для
протонов его величина может достигать нескольких сотен
километров.
Сохранение магнитного момента приводит к тому, что в процессе движения частицы вдоль силовой линии выполняется
соотношение sin2<α /B=const. Отсюда, зная питч-угол α на экваторе,
можно определить напряженность поля Вз в точке отражения:
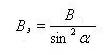
Движение между точками отражения в адиабатическом режиме характеризуется сохранением
Второго, или продольного инварианта который определяется как:
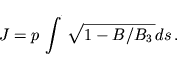
где интеграл берется между зеркальными точками.
В дипольном поле
частицы с разными энергиями и питч-углами, находящиеся на одной
силовой линии, при дрейфе вокруг Земли движутся практически по
одной и той же оболочке (дрейфовой оболочке). Поэтому трехмерное
представление захваченной радиации сводится к двумерному и
характеризуется функцией двух координат: L = Rэ/Rз и В (L-B координаты МакИлвайна).
Для характеристики дрейфовой оболочки удобно пользоваться параметром I, не зависящим от импульса чстицы
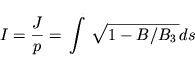
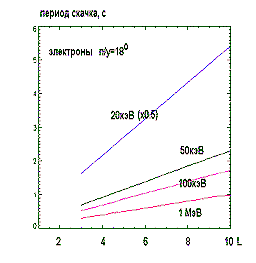
Период колебания частицы между точками отражения удобно расчитывать по формуле
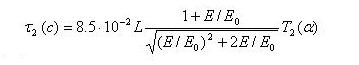
где Т2 (α)= 1,3-0,563 sin αэ.
 | 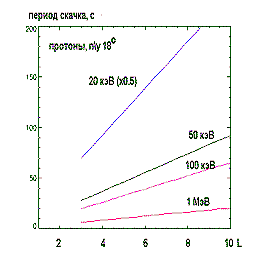 |
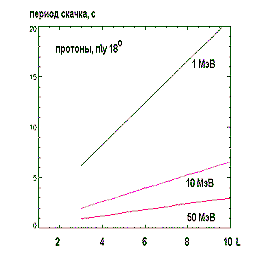 |
Если точка отражения частицы нвходится ниже 100 км, велика вероятность атмосферных потерь. Питч угол частицы
в вершине силовой линии, которую считают погибшей в атмосфере, называется критическим и определяется как
![]()
где Во и Вм напряженность магнитного поля в вершине силовой линии и на высоте 100 км. Область питч-углов меньше критического называют конусом потерь.
Конус потерь лишь приблизительно оценивает реальные потери частиц при питч-угловой диффузии, поскольку граница атмосферы - понятие условное, высота ее колеблется, поглощнение частиц не абсолютно
и т.д. Для дипольного поля величина конуса потерь показана на рисунке и определяется из выражения
![]()
см. вывод формулы
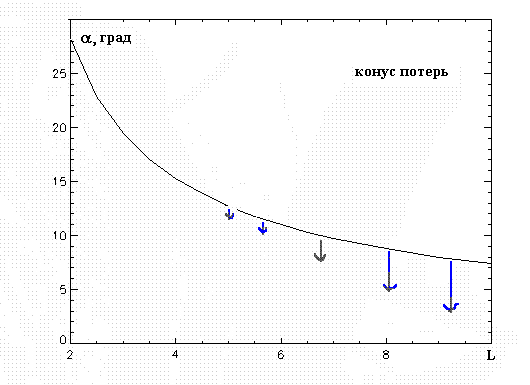
В реальной магнитосфере напряженность поля на экваторе на больших расстояниях меньше дипольного и соответственно, конус потерь меньше, как показано пунктирной линией на этом рисунке.
Третий инвариант Ф определяется как поток геомагнитного поля
через экваториальную плоскость вне данной L-оболочки. При
B/(dB/dt)~τ3 третий инвариант сохраняться не будет, но поскольку
при этом В/(dB/dt) > (τ1 ,τ2), первые два инварианта μ и I
сохраняются. Магнитное поле на данной L-оболочке будет меняться,
при этом E/B=const вследствие сохранения μ, и частица может
перейти на другую L-оболочку с соответствующим изменением Е.
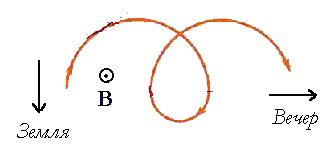 Дрейф вокруг Земли по долготе для частиц с разными знаками
заряда происходит в противоположных направлениях (электроны
движутся на восток, протоны – на запад). Дрейф в магнитном поле имеет немколько разновидностей; в магнитосфере
определяющими являются градиентный дрейф и дрейф из-за кривизны силовых линий (соответственно первый и второй член в правой часи уравнения).
Дрейф вокруг Земли по долготе для частиц с разными знаками
заряда происходит в противоположных направлениях (электроны
движутся на восток, протоны – на запад). Дрейф в магнитном поле имеет немколько разновидностей; в магнитосфере
определяющими являются градиентный дрейф и дрейф из-за кривизны силовых линий (соответственно первый и второй член в правой часи уравнения).
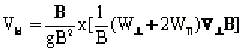
Скорость дрейфа пропорциональна энергии частицы и величине градиента магнитного поля и обратно пропорциональна квадрату напряженности магнитного поля.
Природа градиентного дрейфа
иллюстрируется на рисунке справа.
Период дрейфа вокруг Земли удобно определять из выражения
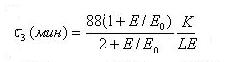
где K= 1,25-0,25 cos 2λm, λm – геомагнитная широта точки
отражения, Е – в МэВ.
Для нерелятивистских частиц τ3= 44/E L
Подробнее о динамике заряженных частиц в радиационных поясах Земли см. в обзоре С.Н. Кузнецова и Л.В. Тверской
из книги "Модель космоса", под редакцией М..И. Панасюка, НИИЯФ МГУ, 2006.
Назад, к оглавлению справочника